OPTIQUE - Optique instrumentale

OPTIQUE - Optique instrumentale

On appelle «instrument d’optique» tout système formant l’image d’un objet sur un ou plusieurs récepteurs sensibles à la lumière et dont le rôle est de percevoir ou d’exploiter cette image. Par exemple, une lunette comporte plusieurs lentilles formant l’image et un récepteur associé, généralement l’œil; la cinématographie fait intervenir deux instruments, la caméra de prise de vues et le projecteur, et quatre récepteurs, les émulsions négative et positive, l’écran de projection et l’œil.

Tout instrument d’optique met donc en jeu trois éléments fondamentaux: l’objet, le système optique et le récepteur (ou les récepteurs).

L’objet est caractérisé par la composition spectrale de la lumière qu’il émet et par la distribution en ses divers points des radiances visuelles ou énergétiques correspondantes, qui détermine la structure spatiale plus ou moins fine de l’image.

Les radiations appartenant au domaine dit optique comprennent: l’ultraviolet, de longueurs d’onde comprises entre 200 et 400 nanomètres (nm); le visible, de 400 à 720 nm (ou 0,72 猪m); l’infrarouge proche de 0,72 à 2 ou 3 猪m; l’infrarouge moyen de 2 ou 3 猪m à 15 猪m et l’infrarouge lointain de 15 à 1 000 猪m. Cette composition spectrale est l’un des facteurs essentiels de l’élaboration de l’instrument. Elle impose les matériaux optiques qui doivent être transparents ou réfléchissants, pour le domaine spectral utilisé, et posséder les combinaisons d’indices de réfraction et de dispersion permettant d’obtenir une bonne image. D’autre part, la distance de l’objet et, pour un récepteur donné, la finesse des détails qu’on désire révéler déterminent le choix des caractéristiques géométriques de l’instrument.

Les récepteurs dépendent principalement du domaine spectral utilisé, et c’est à eux qu’on doit nombre des récents progrès de l’optique instrumentale. Parmi les récepteurs, on peut distinguer:

– L’œil, organe de perception, obligatoirement associé à tout dispositif visuel d’observation et de mesure;

– Divers récepteurs qui, placés dans le plan d’une image, en fournissent une reproduction qui peut être observée par l’œil, permettant à ce dernier d’atteindre des domaines auxquels il n’a pas accès (on peut citer l’émulsion photographique sensible à l’ultraviolet, au visible et au début de l’infrarouge; les convertisseurs d’images électroniques pour l’ultraviolet et l’infrarouge moyen, etc.);

– Enfin, les récepteurs dits «à balayage»; certains de ceux-ci utilisent les méthodes de la télévision, couvrent l’ultraviolet et le visible et s’étendent progressivement vers l’infrarouge moyen; d’autres possèdent un récepteur unique, quasi ponctuel, qui balaye successivement tous les points de l’image, le courant variable produit servant, par exemple, à moduler une lampe qui, au moyen d’un balayage synchrone, reproduit, en chaque point, les intensités de l’image primaire; il existe sur le marché des appareils de ce type permettant d’obtenir les images à la cadence cinématographique normale grâce aux radiations émises par les corps considérés à la température ordinaire.

On peut, par le même procédé, analyser une seule ligne et reproduire le résultat sous forme de courbe (analyseurs de spectres, microphotomètres), ou même signaler le comportement d’un seul objet au milieu de nombreux autres; en général, l’œil n’intervient plus, le signal électrique étant utilisé directement pour effectuer des comptages, des surveillances, des déclenchements d’alarme, des signaux sonores, ou des commandes d’automatisation. Le développement de ces récepteurs a créé une industrie de l’optique instrumentale infrarouge.

1. Association de l’instrument et du récepteur

Relations entre l’objet et l’image instrumentale

Du point de vue de ses performances, un système optique quelconque (fig. 1) est complètement défini par ses pupilles d’entrée P^e et de sortie P^s , de diamètres linéaires 行 et 行 , d’ouvertures angulaires 見 et 見 , les ouvertures numériques objet et image étant donc sin 見 et sin 見 . On doit avoir, entre ces quantités, la relation dite des sinus d’Abbe, qui s’écrit:

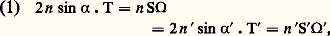où n et n sont les indices de réfraction des milieux objet et image, qui sont égaux à l’unité sauf dans les cas d’instruments travaillant en immersion, T et T étant les dimensions transversales de l’objet et de l’image, S et S les angles sous lesquels ils sont vus.

Par définition, la puissance de l’instrument est P = S /T, et son grossissement G = S /S. Son champ s’exprime par la valeur maximale de T ou de S, ou encore de T ou de S correspondant à des images utilisables.

Lorsque l’objet ou l’image s’éloignent à l’infini, 見 ou 見 tendent vers zéro et T ou T vers l’infini, et on utilise alors les expressions S 行 ou S 行 .

Soit un instrument d’optique qu’on suppose parfait: du fait de l’ouverture limitée de la pupille d’entrée, tout se passe comme si chaque point de l’objet prenait la forme d’une tache de diffraction, respectivement de rayon linéaire et angulaire:

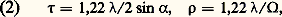où est la longueur d’onde (cf. LUMIÈRE – Diffraction).En ajoutant, pour chaque point de l’objet, les intensités de toutes les taches de diffraction superposées en ce point, on obtient la distribution des éclairements dans l’objet, vu à travers la pupille d’entrée. On appelle «fonction de transfert» celle qui représente le contraste de l’image en ordonnée en fonction de la fréquence spatiale de l’objet en abscisse. Lorsque la fréquence spatiale augmente (ou que la période diminue), le contraste de l’image décroît; il s’annule pour une fréquence dite de coupure, dont l’inverse est la limite de résolution.

On obtient ainsi un «objet optique», qui définit les contrastes les plus élevés qu’on puisse atteindre dans l’observation de l’objet à travers la pupille d’entrée. Dans un espace image quelconque de l’instrument, la distribution des luminances, donc des contrastes, est identique à celle de l’objet optique; les longueurs T et les angles S sont reliés à T et à S par la relation d’Abbe (1). D’autre part, les éclairements sont inversement proportionnels au carré du grandissement 塚 ou au carré du grossissement angulaire G:

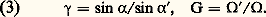Pour un instrument présentant des défauts, on obtient dans l’espace image une distribution d’éclairements provenant des effets combinés de la diffraction des aberrations et des défauts de construction. L’application de la formule d’Abbe à une marche inverse des rayons permet de déduire l’objet optique, donc les performances instrumentales.

Association d’un récepteur à l’image instrumentale

Les images considérées jusqu’ici isolément sont toujours associées à des récepteurs dont le mode d’action est analogue, quelle que soit leur nature; deux facteurs interviennent:

– la structure discontinue de la couche sensible (granularité d’une émulsion, structure d’une image formée par balayage) ou la structure rétinienne;

– la diffusion dans la couche (constituant une tache à éclairement décroissant plus ou moins rapidement du centre au bord); elle peut être d’origine optique (diffusion par un milieu trouble), ou, dans les récepteurs thermiques, être la diffusion de la chaleur dans la couche sensible.

C’est donc une combinaison des taches élémentaires du récepteur et de l’optique de l’instrument qui définit l’image agissant sur les éléments sensibles; le résultat dépend du rapport entre les dimensions des deux taches. Lorsque l’ouverture du faisceau optique est assez petite pour que la tache de diffraction ait un diamètre au moins trois fois supérieur à celui de la tache propre au récepteur, l’effet produit par cette dernière est pratiquement inexistant: le récepteur n’altère pas l’image instrumentale. Dans le cas inverse, ce sont les propriétés optiques du récepteur qui déterminent la netteté de l’image. Entre ces deux limites, on passe progressivement d’un cas à l’autre.

Si g ^a et 福 sont les rayons angulaires, exprimés en radians, des taches de granularité-diffusion et des taches de diffraction et si 諸^g et 諸^d sont les rayons linéaires de la pupille de sortie de l’instrument, on a:

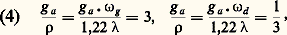d’où:

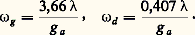Pour l’œil, par exemple, le rayon de la tache de granularité – diffusion – aberrations est égal à 1,2 minute d’arc (3,49 練 10^-4 rd); la longueur d’onde moyenne de la lumière étant de 6 . 10^-4 nm, on trouve 諸^g = 6,3 mm et 諸^d = 0,7 mm.

Le plus grand diamètre pupillaire pour lequel l’œil obéit aux lois de la diffraction est donc voisin de 0,7 mm, et la diffraction n’intervient plus au-delà d’un diamètre de 6 mm, qui n’est atteint que pour des luminances faibles telles que les propriétés de l’image optique perdent leur importance par rapport à la structure rétinienne.

Considérons maintenant les rayons linéaires g ^l et 精 des taches images propres au récepteur et à la diffraction; m ^g et m ^d sont les nombres d’ouverture du faisceau correspondant aux valeurs de g ^l et de 精 définis comme suit:

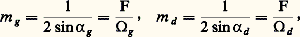où F est la longueur focale de l’instrument et où les nombres m sont ceux qui sont inscrits sur les objectifs photographiques. On aura:

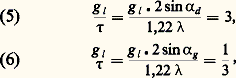d’où: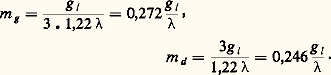

Soit une émulsion photographique pour laquelle g ^l = 30 猪m, = 0,6 猪m et g / = 50; on trouve, par la formule (6), m ^d = 123,3 et m ^g = 13,7.

Pour un objectif de bonne qualité, la résolution sur l’émulsion est donc indépendante du diaphragme, pour les nombres d’ouverture inférieurs à 13,7; c’est l’émulsion qui détermine la netteté de l’image, indépendamment du système optique.

La mesure directe du rayon linéaire de la tache de granularité-diffusion est une opération délicate. On obtient une approximation suffisante en lui donnant une valeur égale à la limite de résolution propre au récepteur, obtenue par un test de Foucault (mire à bandes rectilignes parallèles alternativement claires et sombres d’égale largeur) de contraste égal à l’unité. Pour tous les récepteurs, l’émulsion photographique et l’œil en particulier, ce rayon dépend des conditions expérimentales.

Association de l’œil à un récepteur intermédiaire

L’image peut, suivant les cas, être observée directement à l’œil nu ou agrandie soit par reproduction photographique, soit par un instrument d’optique, loupe ou microscope. La perception visuelle peut être définie par la limite de résolution de l’œil dans son champ objet, limite qui peut être différente de celle de l’œil nu lorsque sa pupille d’entrée est diaphragmée par la pupille de sortie de l’instrument grossissant; suivant les cas, on prendra la limite de résolution angulaire s ou la limite de résolution linéaire t .

On considère deux cas limites, entre lesquels tous les intermédiaires sont possibles.

On désire d’abord une image possédant le mieux possible l’aspect de l’objet vu à l’œil nu; il convient alors que la limite de résolution linéaire du récepteur (égale au rayon g ^g de sa tache de granularité-diffusion) soit vue par l’œil, placé à une distance D, sous un angle n’excédant pas 2 minutes d’arc. Si un objectif, de longueur focale F, photographie un objet à grande distance sur une émulsion dont la tache image propre a un rayon g , la limite de résolution angulaire dans l’espace objet est S = g /F. Soit, par exemple, F = 50 mm (format 24 憐 36), g ¹ = 0,03 mm et g ² = 0,02 mm; on trouve:

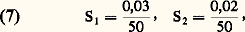soit respectivement 2 minutes et 1,3 minute d’arc. Pour remplir les conditions énoncées, l’image devra être observée à l’œil nu à travers une lentille de 50 mm de distance focale, à la distance conventionnelle de 250 mm; il faudra l’agrandir cinq fois.

On désire ensuite, dans un deuxième cas, obtenir de l’image le maximum d’informations ou la meilleure précision de mesure. Il convient alors que la tache de granularité-diffusion du récepteur de rayon g soit vue par l’œil sous un angle 兀 compris entre 6 et 10 minutes d’arc; alors, la distribution des éclairements dans l’image du récepteur n’est pas perturbée par les défauts du système optique de l’œil. Soit g = 0,03 mm et 兀 = 6 minutes d’arc, par exemple; on trouve la distance D à laquelle doit se faire l’observation:

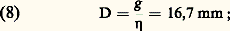le grossissement de l’image est alors:

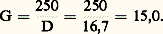2. Perception par les instruments visuels

Schéma de l’instrument visuel

On appelle «instrument visuel» celui dont l’œil constitue le récepteur unique. L’œil ^{[cf. ×IL HUMAIN]} comporte un système optique muni d’un diaphragme à ouverture réglable, l’iris , formant l’image sur une mosaïque de cellules sensibles à la lumière, la rétine , dont les réponses sont transmises au cerveau qui en assure la perception.

Tout instrument visuel (lunette, télescope, microscope, projecteur de profil, etc.) se compose, sous sa forme la plus simple (fig. 2 a et 2 b), d’un objectif Ob formant une image de l’objet et d’un oculaire Oc, dont le rôle est, d’une part, de faire passer dans la pupille d’entrée de l’œil la totalité des faisceaux ayant formé l’image et, d’autre part, de grossir cette image. L’œil devra donc, pour voir l’image entière, faire coïncider sa pupille avec la pupille de sortie de l’instrument. appelée aussi «disque oculaire».

Propriétés de l’œil

Les performances instrumentales S ou T se déduisent des limites de résolution angulaires s de l’œil, relatives à sa pupille d’entrée de diamètre 諸, par la formule d’Abbe (1), qui devient:

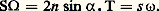Un cas particulier peut se présenter, le cas où la limite s ⁿ correspond au diamètre pupillaire naturel 諸ⁿ .

Lorsque la pupille de sortie de l’instrument est plus petite que celle de l’œil, l’instrument travaille avec ses ouvertures de construction, que nous désignons par O, 2n sin 益 et o, et diaphragme la pupille de l’œil; on a alors 行 = O.

Lorsque 諸 諒 o, la pupille de l’œil diaphragme le disque oculaire, donc l’objectif, avec:

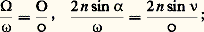on a alors:

La limite de résolution de l’œil est mesurée sur une mire de Foucault, de période et de contraste C variables. Si L^F est la luminance du fond et L^obj celle de l’objet, on a, par définition,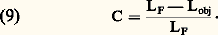

Les figures 3 et 4 montrent les courbes s = f ( 諸) et s 諸 = f ( 諸) pour deux luminances diurnes du test et plusieurs contrastes.

La formule empirique suivante fournit une bonne approximation des valeurs de s 諸 en millimètres multipliés par des minutes d’arc dont on déduit facilement celles de s . Soit C le contraste, 諸^m le diamètre pupillaire optimal, correspondant au minimum de s 諸 (fig. 4); on prendra: 諸^m = 0,75 mm. La formule est valable pour des luminances du test plus grandes que 100 cd/m² (100 candelas par mètre carré):

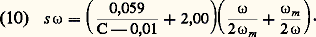Performances d’un instrument visuel optiquement parfait

Les limites de résolution de l’instrument parfait dans son champ objet, limite angulaire S et limite linéaire T, sont reliées à la limite angulaire s de résolution de l’œil: dans le champ image par les formules d’Abbe :

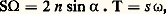d’où: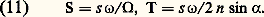

La formule en S est valable pour les objets éloignés et la formule en T pour les objets situés à courte distance de l’objectif.

Relations entre les performances et les caractéristiques géométriques

Soit un système afocal (c’est-à-dire donnant d’un objet à l’infini une image à l’infini), F étant la longueur focale de l’objectif, f celle de l’oculaire et G le grossissement angulaire. On a:

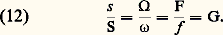Les performances instrumentales désirées dans le champ objet et celles de l’œil dans le champ image définissent les diamètres des pupilles d’entrée et de sortie, donc le grossissement et le rapport des longueurs focales. Celles-ci sont fixées par un compromis entre l’encombrement et la limitation des ouvertures numériques imposée par la correction des aberrations.

Dans le cas d’un objet à distance finie, G^C est le rapport entre l’angle sous-tendu par l’image à l’infini d’une petite longueur objet dy et l’angle sous-tendu par l’objet dy vu à la distance conventionnelle de 250 mm.

Si 塚 est le grandissement de l’objectif f ^oc la longueur focale de l’oculaire et g ^oc son grossissement, on a:

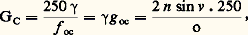pour o 麗 諸ⁿ et où f ^oc et o sont exprimés en millimètres. La puissance 神, exprimée en dioptries 嗀, est l’inverse de la longueur focale équivalente de l’instrument f ^e exprimée en mètres. On a:

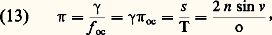pour o 麗 諸ⁿ et où f ^oc et o sont exprimés en mètres. Par exemple, pour un microscope d’objectif 塚 = 50, où f ^oc = 12,5 mm et où g ^oc = 250/12,5 = 20, on a:

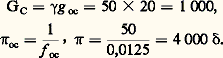Instruments optimaux

Variations de la limite de résolution avec le grossissement

Si 諸 est inférieur à o, l’œil travaille avec sa pupille naturelle 諸ⁿ et la limite de résolution correspondante est s ⁿ . En remplaçant dans les formules (11) donnant les limites de résolution 行 et 2 n sin 見 par leurs valeurs en fonction des données de construction O et sin 益, on obtient:

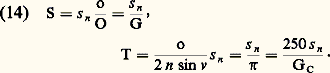La limite de résolution est donc inversement proportionnelle au grossissement ou à la puissance 神. Si 諸 est supérieur à o, on a:

où S est exprimé en radians, T et s 諸 en millimètres et où 行 et 2 n sin 見 sont constants.

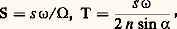La limite de résolution varie comme s 諸, dont les valeurs sont données, pour des luminances diurnes, par les courbes de la figure 4 et la formule (10); les courbes présentent un minimum très accusé correspondant à des valeurs telles que 0,5 麗 諸^m 麗 0,8 mm. Donc, la plus petite limite de résolution est obtenue pour un grossissement optimal G^m . Il en résulte que, dans la pratique, le grossissement optimal des instruments afocaux doit être compris entre 1,25 憐 O et 2,00 憐 O, avec O mesuré en millimètres; les instruments pour objets proches doivent avoir un grossissement commercial maximal compris entre 625 n sin 益 et 1 000 n sin 益 et leur puissance optimale doit être comprise entre 2 500 n sin 益 et 4 000 n sin 益. Le diamètre de la tache de diffraction:

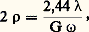correspondant à 諸ⁿ , est alors compris entre 5 et 8 minutes d’arc; il dépend de la longueur d’onde de la lumière et non des défauts géométriques de l’optique oculaire et de la structure rétinienne. Des mesures sur diatomées effectuées au microscope ont montré que la limite de résolution est divisée par un facteur 1,5 quand on passe de l’éclairage en lumière blanche à l’éclairage monochromatique d’une longueur d’onde de 405 nm. Cet effet disparaît pratiquement dès que 諸 閭 1,2 mm.

Variation de la limite de résolution avec l’ouverture pour un grossissement imposé

Si 諸 諒 o, la perception ne change pas quand l’ouverture varie, et il n’y a pas, à ce point de vue, intérêt à augmenter o; si 諸 礪 o, on a:

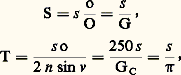avec G, G^C et 神 constants. S et T varient comme s . Dans le domaine des luminances diurnes, la meilleure vision des contrastes faibles, la plus importante pour les instruments d’observation, comporte des valeurs de 諸 variant de 2 à 5 mm suivant la luminance.

Le tableau ci-après fournit, pour une luminance diurne (1 500 cd/m²), pour une luminance située au début du domaine mésopique (1 cd/m²) et pour une autre à la fin du mésopique (10^-2 cd/m²), les diamètres des pupilles de sortie des instruments donnant les meilleures performances.

Lorsqu’on compare deux instruments optimaux de mêmes performances, l’un appartenant au type à ouverture imposée, l’autre à celui de grossissement imposé, un calcul, que nous ne pouvons reproduire ici, indique que leurs caractéristiques géométriques sont très différentes; par exemple, O = 100 mm et G = 133 pour l’instrument optimal à ouverture imposée, alors que l’instrument optimal à grossissement imposé donne O = 153 mm et G = 76. Soit 見 le demi-angle de champ image imposé par l’oculaire, 見 le demi-champ objet et G le grossissement, on a:

À performances égales, le deuxième instrument possédera un champ objet double de celui du premier.

3. Structures instrumentales

Les instruments visuels les plus simples sont conformes à la figure 2; nous renvoyons aux articles LUNETTES ASTRONOMIQUES ET TÉLESCOPES, MESURE – Mesures optiques, MICROSCOPES objectifs PHOTOGRAPHIQUES, pour n’envisager ici que les lunettes terrestres, les périscopes et les endoscopes.

Redressement des images

Le redressement de l’image peut être obtenu soit par une combinaison de surfaces réfléchissantes, soit par un «véhicule».

Redressement par surfaces planes réfléchissantes

On utilise le plus souvent des prismes à réflexion totale, beaucoup plus faciles à monter et à conserver que les miroirs; ces derniers sont cependant parfois utilisés.

Il faut d’abord citer les combinaisons de Porro. Le système de Porro se compose de deux ensembles de deux surfaces perpendiculaires entre elles, dont les deux arêtes d’intersection sont également perpendiculaires entre elles. Dans la première espèce, le rayon incident sur la première face est parallèle au rayon émergent de la deuxième face (fig. 5). Pour la seconde espèce, le rayon réfléchi par la deuxième face est perpendiculaire au rayon incident sur la première. Un quelconque des quatre prismes élémentaires peut être séparé des autres à condition qu’on ne change pas son orientation. La combinaison de Porro est de loin la plus usitée.

Les prismes de la figure 6 (a, b, c) redressent totalement l’image. Leur inconvénient est d’être difficile à construire et d’avoir de plus longs trajets dans le verre: on y a joint le prisme rhomboèdre, qui déplace latéralement le faisceau sans changer l’orientation de l’image.

Les figures 7 a et 7 b schématisent un corps de jumelles à prismes et un corps de jumelles périscopiques, l’un et l’autre composés d’un objectif et d’un oculaire auxquels est joint un système de Porro.

Les jumelles commerciales ont des grossissements égaux à 4, 6, 8, 12 ou 16, les plus fréquents étant 6 et 8. Le plus souvent, le diamètre du disque oculaire est voisin de 3,3 mm, le champ image étant de 50⁰ à 55⁰. Il atteint 65⁰ pour les jumelles à grand champ et 85⁰ pour les oculaires munis de surfaces asphériques. Les instruments permettant une vision au crépuscule et pendant la nuit possèdent des disques oculaires de 6 à 8 millimètres. Le réglage de l’écart d’yeux est effectué par rotation des corps autour d’un même axe. Pour les instruments militaires lourds, on préfère souvent déplacer l’un des corps parallèlement à l’autre. Lorsque le diamètre de l’objectif dépasse celui de l’écart d’yeux, on rapproche les axes optiques au moyen de deux rhomboèdres dont la rotation autour de l’axe optique fait varier l’écart d’yeux.

On peut rattacher à ces instruments de nombreux appareils de topographie et de géodésie, les diverses lunettes de visée, les appareils de pointage, certains étant agencés pour faire le tour complet de l’horizon sans déplacement du pointeur (types panoramiques), les lunettes de tir au fusil et de chasse.

La mise au point de tous les instruments de nuit doit être modifiée systématiquement de 漣 1,5 dioptrie afin qu’ils soient adaptés à la myopie de nuit des utilisateurs.

Redressement par véhicule

Un véhicule est un système composé de deux lentilles, V¹ et V² (fig. 8), et fournit une image renversée I² de l’image I¹ formée par l’objectif Ob. L’image I², droite par rapport à l’objet, est observée à l’aide d’un oculaire Oc et l’ensemble porte le nom d’oculaire terrestre.

Le véhicule allonge les instruments; lorsque cela ne présente pas d’inconvénients, ce système est avantageux parce que beaucoup moins coûteux que les prismes, en particulier pour la chasse de nuit, et dans des instruments périscopiques de petites dimensions. Il est utilisé systématiquement dans les périscopes et les endoscopes pour obtenir la plus grande longueur possible.

Allongement des instruments

L’observation ou la surveillance d’objets inaccessibles ou dangereux exige des instruments de performances modestes, en général, mais dont la longueur peut être considérable: c’est le cas des périscopes ainsi que des endoscopes médicaux ou industriels. Deux procédés sont utilisés: transport d’image par véhicule, avec œil de chat et renversement d’image, et transport par système afocal associé à un objectif.

Transport d’image par véhicule

La figure 9 représente le schéma de principe d’un périscope (objet à l’infini). L’objectif, de longueur focale f ^ob, forme l’image, de rayon y ¹, sur le verre de champ C¹; un véhicule, composé de deux lentilles V¹ et V², de longueurs focales f ^V1 et f ^V2, séparées par un intervalle T, appelé longueur de transport, forme l’image de C¹ en C²; si la longueur totale du système est suffisante, on observe l’image intermédiaire avec un oculaire. Sinon, on introduit des systèmes identiques à V¹, V², C² en nombre suffisant.

On trouve pour le grossissement angulaire G: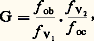

avec O = G 憐 o, O et o étant les diamètres des pupilles d’entrée et de sortie. Si y ¹ est le diamètre de l’image fournie par l’objectif et si u est le demi-angle de champ, on a:

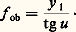La marche des rayons obliques (fig. 9) montre que la largeur du faisceau incliné situé entre les véhicules est d’autant plus faible que le transport T est plus long. La pupille située au milieu de la distance entre les véhicules représente la partie commune à deux cercles de rayon d /2, dont la distance suivant la ligne des centres est égale à BC (fig. 9). Soit d le diamètre libre des lentilles du véhicules et y ¹ le rayon de l’image objective; si on appelle 猪 le rapport BC/AC, on obtient:

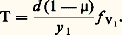On admet alors que l’observateur ne remarque pas l’assombrissement progressif de l’image vers le bord, pour 猪 = 0,3. Prenons y ¹ = 30 mm, f ^V1 = 2 000 mm et d = 120 mm; on trouve T = 5 600 mm (périscope de sous-marin).

L’allongement obtenu est considérable. Ce qui précède s’applique de la même manière à partir de l’image formée en C¹. Le cas de l’objectif sera examiné plus loin.

Transport d’image par association d’un système afocal à un objectif

Soit (fig. 10) y le diamètre libre des lentilles, constant sur toute la longueur du tube, entre l’entrée E et la sortie S de l’instrument; le champ de demi-angle u étant imposé, f ^ob est beaucoup plus petite que la distance ES. On procède comme suit pour obtenir en S une image possédant le champ voulu: on choisit un objectif Ob dont la pupille d’entrée soit située en E, et de longueur focale telle que son image I se forme en S; l’image étant beaucoup trop grande, le champ est réduit; pour obtenir, sans changer la position de l’image, un champ k fois plus grand, correspondant à une longueur focale k fois plus petite, on place devant l’objectif Ob un système afocal L¹L², de grossissement G^a = 1/k inférieur à 1 (lunette à l’envers). Le demi-champ primitif étant u , le champ nouveau u ^k s’en déduit par:

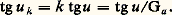La longueur focale de l’objectif muni de L¹L² est alors:

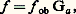l’image étant restée à la même place. On utilise presque exclusivement, comme système afocal, des lunettes de Galilée inversées qui ont le double avantage de ne pas renverser les images et d’introduire une lentille divergente puissante qui apporte des surcorrections d’astigmatisme et de courbure de champ améliorant beaucoup la qualité des images; la pupille d’entrée, quant à elle, est virtuelle et située entre les deux lentilles.

Endoscopes: objectifs

Soit un endoscope (fig. 11), comprenant un objectif Ob et un ou plusieurs véhicules donnant de l’objet de longueur y , situé à une distance d de l’objectif, une image y observée par l’oculaire Oc de grossissement g ^oc = 250 mm/f ^oc. On a les formules connues, donnant le grossissement commercial:

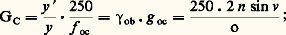on en déduit le diamètre O de la pupille d’entrée de l’objectif O = 2 d sin v .

Prenons, par exemple, les mesures des instruments médicaux: G^C = 1, d = 50 mm, o = 2 mm, n = 1,3. La relation donnant G^C en fonction de sin v fournit sin v , qui donne O par la relation O = 2 d sin v . En supposant le nombre d’ouverture des lentilles constant m = 10, on trouve f ^oc = 20 mm et d ^ob = 3,1 mm. Connaissant d et d , on en déduit f ^ob par les formules de Gauss et on trouve f ^ob = 2,91 mm. La connaissance de O permet d’obtenir les performances visuelles et les performances sur récepteur intermédiaire.

Endoscopes: redressement de l’image et éclairage de l’objet

Quand on utilise un endoscope, l’œil examine les images suivant l’axe de l’instrument, et il est indispensable qu’elles soient semblables à l’objet, sans inversion de la droite et de la gauche. Cela nécessite deux réflexions, obtenues le plus souvent par un prisme à réflexion totale à surfaces réfléchissantes «en toit».

L’éclairage des objets endoscopiques est presque toujours indispensable; il est effectué en plaçant une lampe en avant de l’objectif; lorsque l’instrument travaille en bout, on munit cette lampe d’un écran empêchant le faisceau direct de pénétrer dans l’objectif; lorsque l’instrument observe latéralement, la lampe est disposée de manière à éclairer le mieux possible le champ. Jacques Vulmière utilise un «guide de lumière», cylindre de silice polie, très transparent: l’image de la source est projetée à l’entrée, et le flux qui est entré se retrouve presque intégralement à la sortie soit directement, soit orienté par un prisme.

Périscopes et endoscopes industriels

Périscopes

Les périscopes sont des instruments dont la disposition et la longueur sont prévues pour surveiller des lieux ou des objets dont l’observateur ne peut s’approcher soit parce qu’ils sont dangereux, soit parce qu’ils sont hors de sa portée. Les plus connus sont les instruments militaires, permettant de voir en restant dissimulé et protégé; périscopes de sous-marins, de chars, de tranchées et de fortifications. Récemment, des appareils ont été réalisés pour la surveillance d’appareils manipulant des combustibles nucléaires, de machines ioniques ou électriques à très hautes tensions, pour la lecture d’appareils de contrôle et pour la surveillance d’organes difficilement accessibles et d’ouvrages sous-marins peu profonds.

Les instruments de grande taille sont composés (fig. 12) d’un «petit tube», de diamètre extérieur de l’ordre de 50 mm, la longueur allant de quelques centimètres à 1 m. Ce tube contient le prisme de tête, l’objectif et son verre de champ, se raccordant par un cône à un tube d’un plus grand diamètre (15 à 30 cm); celui-ci est choisi de manière à pouvoir assurer la longueur de transport au moyen d’un seul véhicule, suivi du prisme de pied et de l’oculaire.

Lorsque l’instrument peut pivoter autour de son axe vertical, il est possible d’obtenir la vision d’un point quelconque de l’espace en faisant tourner le prisme de tête autour d’un axe horizontal, ce qui permet de déplacer l’axe optique d’une centaine de degrés. Lorsque l’instrument est fixe, l’exploration en azimut est effectuée par rotation de la tête de l’instrument, munie d’un système de prismes maintenant l’image droite. La longueur de ces instruments peut varier de deux à trois mètres jusqu’à une quinzaine de mètres.

La réalisation d’appareils de grandes dimensions pose des problèmes de construction optique et mécanique très difficiles que nous ne pouvons traiter ici. On doit cependant signaler que les grands périscopes, dont la transparence était voisine de 14 p. 100 avant l’existence des traitements antiréfléchissants, transmettent actuellement, en combinant ces traitements avec l’emploi de verres très transparents, plus de 50 p. 100 de la lumière qu’ils reçoivent.

Les petits instruments, de un à deux mètres de longueur, présentent les mêmes particularités de construction que les instruments courants.

Du point de vue des caractéristiques géométriques, le grossissement de 1,5 donnant, en vision monoculaire, le même aspect que la vision binoculaire à l’œil nu, est le plus fréquent, avec des champs images et des diamètres de disques oculaires analogues à ceux des jumelles à prismes. Dans les instruments à petit tube, l’introduction d’une lunette de Galilée inversée est de règle. On emploie aussi le grossissement 6, l’objectif étant le plus souvent analogue à un objectif de jumelles à prismes (deux verres collés); on le transforme en grossissement 1,5 par l’adjonction d’une lunette de Galilée inversée escamotable.

Endoscopes industriels

Les endoscopes industriels sont utilisés couramment pour le contrôle des défauts de matière et d’usinage à l’intérieur des tubes et de réservoirs destinés à supporter de très hautes pressions, pour la surveillance de l’altération de contacts dans l’huile et pour la surveillance d’arcs électriques à forte intensité, etc. Le modèle le plus répandu comporte un certain nombre de tubes de un mètre environ de longueur, qui peuvent se raccorder pour former un ensemble atteignant parfois quatre à cinq mètres. Le premier tube constitue un endoscope complet et les autres contiennent chacun un véhicule et un verre de champ. Le grossissement moyen est voisin de 1,5 lorsque le disque oculaire est de l’ordre de deux millimètres. Le diamètre extérieur, constant, varie entre trois et cinq centimètres. Pour des cavités plus étroites, on emploie les endoscopes médicaux. Ceux-ci prennent une importance sans cesse croissante pour les examens des cavités internes du corps humain (cystoscopes; œsophagoscopes, bronchoscopes, etc.) ou d’organes quelconques, l’instrument étant amené en contact avec ces derniers par l’intermédiaire d’un tube perforateur (examen du foie, exploration et conduite d’opérations à l’intérieur du cerveau). Les caractéristiques optiques sont déterminées par un diamètre de disque oculaire de deux millimètres et un grossissement voisin de 1, pour une distance d’observation de cinquante millimètres.

Problèmes de construction

La construction des instruments précédents exige des précautions spéciales. La correction des aberrations est analogue pour tous les instruments visuels.

Objectifs

Les objectifs sont presque toujours à deux verres, collés ou non, et corrigés des aberrations chromatiques et sphériques sur l’axe; ils satisfont en outre à la condition des sinus; par contre, on ne peut agir sur leurs aberrations extra-axiales. Les verres des véhicules se traitent comme ceux des objectifs. Dès que leur diamètre dépasse 80 mm, les résidus de chromatisme (spectre secondaire) d’objectifs, par ailleurs bien corrigés, obligent à les utiliser avec des nombres d’ouverture m élevés ou, sinon, à tolérer des dégradations importantes de l’image; c’est ce qui arrive dans les véhicules des grands périscopes, et, a fortiori, pour les objectifs d’observatoires. André Couder donne les formules suivantes de tolérances.

Soit F la longueur focale mesurée en mètres et D le diamètre mesuré en centimètres, on a:

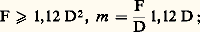et, si D est égal à 10 cm ou à 50 cm, on a respectivement:

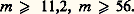On a intérêt, pour limiter l’encombrement des instruments, à diminuer le plus possible les longueurs focales, donc à augmenter les ouvertures. Actuellement, pour des diamètres d’objectifs de quelques centimètres, on ne dépasse pas le nombre d’ouverture m = 4. Il existe cependant des objectifs, ouverts à f /3 et même à f /2, comportant une surface parabolique.

Oculaires

Les formes classiques des oculaires de Huygens et de Ramsden ne peuvent convenir que pour m 礪 10 (sinon les aberrations sphériques et chromatiques sont trop fortes), et pour des champs ne dépassant pas 30⁰ à 35⁰.

La forme la plus fréquente est la forme de l’oculaire de Kellner, dérivé de celui de Ramsden, avec un verre de champ plan convexe et un verre d’œil achromatique. On trouve aussi la disposition inverse, verre de champ achromatique et verre d’œil plan convexe. Les champs obtenus peuvent atteindre 65⁰ avec 6 dioptries d’astigmatisme au bord et 85⁰ avec 12 dioptries. Les caractéristiques de ces oculaires diffèrent notablement de celles des oculaires de Huygens et de Ramsden, parce qu’ils doivent non seulement posséder un champ plus étendu, mais encore, le plus souvent, compenser en partie les aberrations extra-axiales des objectifs.

Les aberrations essentielles à corriger sont: le chromatisme latéral, la courbure de champ et la distorsion, cette dernière devant rester faible pour ne pas fatiguer le système d’accommodation de l’œil (face=F0019 麗 0,5 dioptrie). L’introduction des surfaces asphériques de Lacomme a permis d’atteindre des champs de 90⁰ avec moins de trois dioptries d’astigmatisme au bord. Enfin, il est essentiel que, pour des instruments à grands disques oculaires, l’imagerie pupillaire soit le mieux possible corrigée de l’aberration sphérique et de la coma.

Défauts de construction

Tout instrument d’optique comporte deux groupes d’éléments dont l’association pose les problèmes majeurs de la construction: le système optique et la mécanique, à laquelle est dévolu le rôle de maintenir les pièces optiques d’une manière permanente dans les positions qui leur sont assignées par le calcul, en supprimant au mieux les dilatations, les flexions et les jeux. Toute erreur ou tout déplacement, introduisant des défauts de centrage ou un changement dans la position des surfaces ou leur déformation, peuvent rendre inutilisable un instrument en lui-même parfait.

Une première catégorie de défauts optiques est celle qui altère la forme de la surface d’onde; elle provient soit des erreurs de taille des surfaces, soit des défauts d’homogénéité du verre, c’est-à-dire de variations faibles et irrégulières de l’indice de réfraction et de la biréfringence.

Un autre défaut est dû à la lumière parasite qui, malgré les précautions prises pour l’éliminer, fait subir à l’image une perte de contraste qui dépasse le plus souvent celle qui résulte des résidus d’aberrations; les traitements antiréfléchissants, outre l’augmentation de la transparence qu’ils apportent, diminuent dans des proportions considérables la lumière parasite provenant des réflexions par les lentilles; il reste cependant celle qui est produite par l’intérieur de l’instrument, et dont l’élimination correspond à l’une des phases les plus importantes des études mécaniques.

Encyclopédie Universelle. 2012.